こんにちは!じゃがいも先生です🥔✨
2次不等式を解いているとき、こんな経験はありませんか?
\(x^2-2x+5=0\) を解いたら
\(x=1\pm\sqrt{-4}\) や、\(D=-4<0\)
答えは「解なし」だ!
と思って、答えを見ると「すべての実数」になっている。
えっ?解なしなのに、すべての実数??
今回はこの「矛盾してるようで矛盾してない」理由を、グラフを使ってやさしく説明します!
【結論】「解なし」でも「すべての実数」になるのは“意味が違う”から!
👉「解なし」でも「すべての実数」となるのは、考えている問題が違うからなんです。
つまり、「方程式の解なし」と「不等式の解なし」は意味が違うのです。
【理由】解の公式や判別式の「解なし」は“グラフとx軸が交わらない”こと
まず、解の公式や判別式\(D\)で出てくる「解なし」は、
グラフとx軸が交わらないことを表しています。
たとえば、\(y=x^2+6x+8\) が
\(x\)軸がぶつかる点を求めるには \(x^2+6x+8=0\) を解きます。
\begin{align}
&x^2+6x+8&=0\\
\\
&(x-2)(x-4)&=0\\
\\
&よって、x=2,4
\end{align}
この2つの点が、グラフとx軸が交わる場所です。
では、今回の問題
\(x^2-2x+5=0\)
を考えてみましょう。
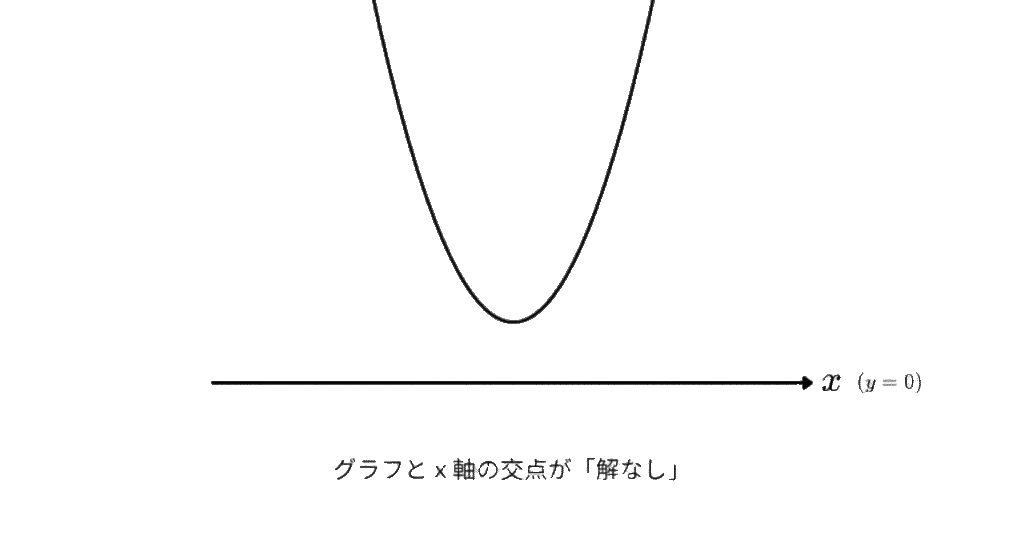
これを解いて出てくる、「解なし」は
グラフと \(y=0\) つまり \(x\) 軸が「ぶつからない」ということ。
つまり、
解の公式や判別式の「解なし」…x軸と交点がない。
という意味なんです。
【例題】グラフで見る「解なし」と「すべての実数」の違い
ではここからが本題です。
「不等式」では、この“ぶつからない”グラフをどう考えるのでしょうか?
ケース①:>0のときは「すべての実数」になる理由
2次不等式 \(x^2-2x+5>0\)
2次不等式 \(x^2-2x+5>0\) では
グラフ \(y=x^2-2x+5\) が、\(y=0\)(\(x\)軸)より大きく(>0)なるときの \(x\) について考えます。
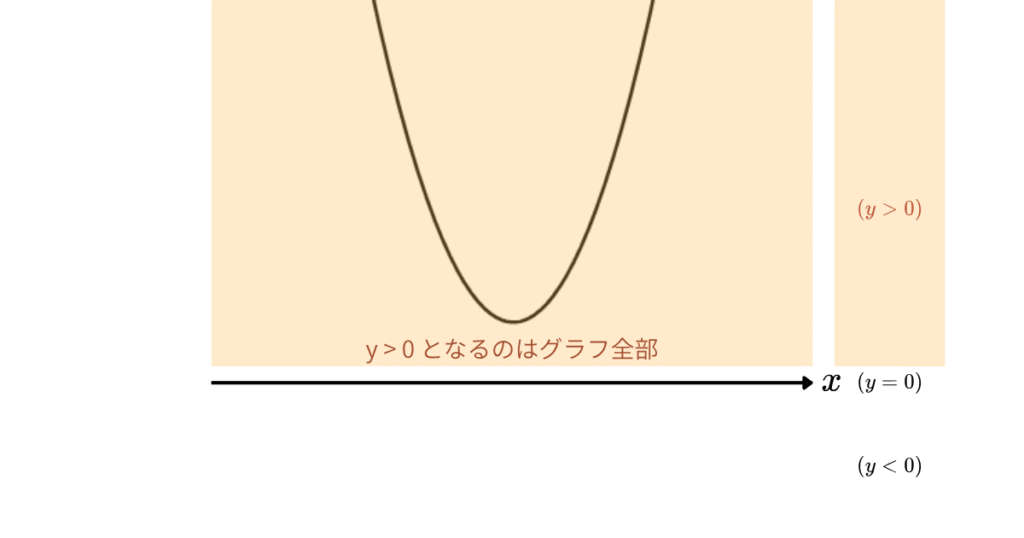
グラフ \(y=x^2-2x+5\) は、x軸よりずっと上にあります。
x軸とぶつかっていない…常にy>0ということ。
だから、この不等式を満たす \(x\) は
✅ すべての実数
となります。
つまり「 \(x\) がどんな値でも、\(y\) は \(0\) より大きい」のです。
ケース②:<0のときは「実数解なし」になる理由
2次不等式 \(x^2-2x+5<0\)
今度は不等号の向きが逆。
「グラフがx軸より下にあるとき」を探します。
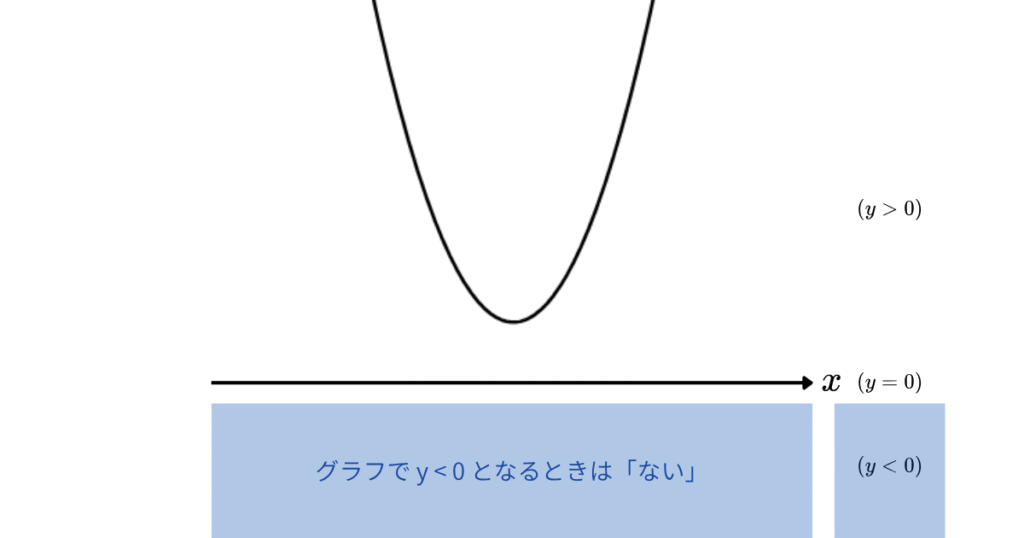
でも、このグラフはx軸にすら触れません。
ずっと上を通っているので、yが0より小さくなることは一度もありません。
❌ そんなxは存在しない(実数解なし)
となるわけです。
【まとめ】2次不等式では「=」「>」「<」で答えが変わる!
ここまでの内容を整理すると…
| 式 | 考えていること | 答え |
|---|---|---|
| \(x^2-2x+5=0\) | グラフとx軸がぶつかるときのx | 解なし |
| \(x^2-2x+5>0\) | グラフがx軸より上になるx | すべての実数 |
| \(x^2-2x+5<0\) | グラフがx軸より下になるx | 解なし |
つまり、同じ式でも「=」「>」「<」で結果がまったく変わるのです。
【会話で復習】「解なし」と「すべての実数」はどう違う?
 にんじん君
にんじん君先生、「解なし」って言われると、もう全部ダメな気がしてました…!

いい質問だね。実は“どこにも交点がない”ってだけなんだよ
 にんじん君
にんじん君なるほど!不等式だと、グラフの上か下かを見てるんですね!

そう!だから“解なし”でも、“すべての実数”になることがあるんだ。
グラフで考えるとスッキリするでしょ?
【ポイント整理】「グラフとx軸の関係」をイメージすれば迷わない!
2次不等式を解くときは、
「グラフとx軸の関係」をイメージするのがポイントです🌾
「解なし」と見えても、もしかしたらそれは**“常に正しい”不等式**かもしれません。
ぜひグラフを描いて、確かめてみてくださいね!


コメント